遠い星ほど暗い?
月が2倍遠くなった時を考えましょう。カメラのレンズ、または眼球の水晶体に当たる月からの光のエネルギーは距離の2乗に比例するため、月からの光のエネルギーは1/4になります。一方、カメラのCCDまたは、眼の網膜に写る月の大きさは半分になります。面積はその2乗ですから、1/4になります。月が2倍遠くなった時、レンズにあたるエネルギーは1/4ですが、それが1/4の面積のCCDや網膜に集まるわけですから、月の像の単位面積当たりのエネルギーは変わらないことになります(1/4÷1/4=1)。ですから、2倍、4倍、10倍でも同じことが言えます。すなわち、星が遠くなっても、レンズが結ぶ星の像の明るさは変わらないのです。
ところが、実際には、「遠い恒星ほど暗い」(星自身の明るさが同じでも)と言われています。何故でしょう。それは、いくら星が遠くなっても、レンズのぼけや、CCD、網膜の光を受ける最小単位のために、ある程度以上には像が小さくならないからです。つまり、ある程度遠い場合、像の面積が変わらず、レンズに当たるエネルギーだけ距離の2乗に比例して少なくなるため暗くなってしまうのです。
結論は、ある程度以上の大きさの像を結ぶ範囲内で、星の明るさは変わらないが、それ以上になると、距離の2乗に比例して暗くなると言えます。
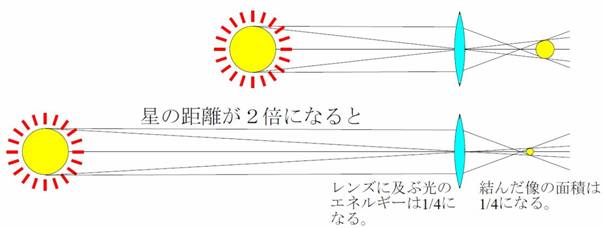
1/4のエネルギーが1/4の面積に像を結ぶので、像の単位面積当たりの光の強度は変わらない。